Coloring adjacent regions of a circle with n chords using 2 colors

January 12, 2025

I came across this problem in the book How to Prove It: A Structured Approach and the solution turned out to be really neat, so I wanted to make a short post about it.

Let n be a positive integer, and suppose n chords are drawn in a circle, cutting the circle into a number of regions. Prove that the regions can be colored with two colors in such a way that adjacent regions (that is, regions that share an edge) are different colors.

I've made a demo below. Just click on the circle to add a new line and re-color the regions! Refresh the page to reset.

Click the circle to add a new line and re-color the regions. Refresh the page to reset.

This is the proof, by induction. (it's the same as in the link above, just explained in a little more detail):

For the base case, n = 1, if you have a circle with a single chord, then there are only 2 regions, so you can clearly make each region a different color.

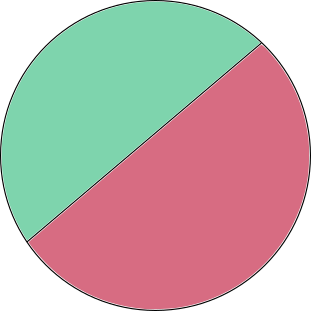
An image of a circle with one chord, and both regions are different colors. — Base case

Then for the induction step, suppose you have a circle with n chords drawn through it, colored such that each adjacent region is a different color.

An image of a circle with 3 chords, colored so that each adjacent region is a different color. — Induction hypothesis, every adjacent region is a different color

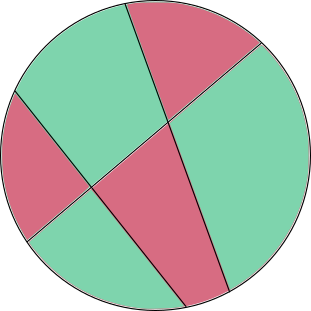
Now add a new chord to the circle so that there are n + 1 chords. Then you'll notice that the only regions that are the same color are those that were previously the same region before adding the new chord.

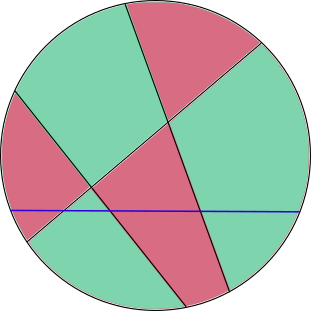
The same circle from above except with a blue line added through it, which creates some adjacent regions with the same color. — Add a new chord (in blue)

Now just take every region on one side of the new chord and swap the color of the region.

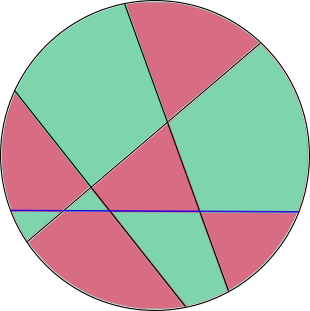
The circle is now re-colored such that each adjacent region is a different color again. — Swap the color of every region below the blue chord. And we're done!

Now every adjacent region in the circle is a different color again.

To explain why this works, consider any two adjacent regions in the circle. Either the regions are both on the same side of the new chord, or they're on opposite sides of the new chord. We'll consider each case separately:

If the regions are on the same side of the new chord, then they were already adjacent before adding the chord, and so must have been different colors. The regions are either on the side of the chord where we swapped all the colors, or the side that we didn't touch. If they're on the side we didn't touch, then they must still be different colors as before. And if they're on the side where we swapped the colors, then note that the colors of both regions would have changed, so they would also be different colors.

If the regions are on opposite sides of the new chord, then they would have been the same color right after the new chord was added. But since we changed the color of every region on one side of the chord, then these two regions must now be different colors.

This shows that after adding a new chord, you can always re-color the circle so that no two adjacent regions have the same color.

This concludes the proof because if you're given a circle with n chords, you can start with an empty circle and then add each chord one at a time, using the steps above to re-color the circle after each new chord.